

Given: Ð1 and Ð2 are supplementary Ð3 and Ð4 are supplementary Ð4 Prove: Ð3 1 2 4 3 Statements Reasons 1. Substitutionĩ YOU CANNOT UNDER ANY CIRCUMSTANCES USE THE REASON “DEFINITION OF VERTICAL ANGLES”ġ0 Ð1 and Ð2 are supplementary Ð3 and Ð4 are supplementary Ð2 Ð4 Substitution You can also say “Vertical Angle Theorem” 4. Given You can also say “Vertical Angle Theorem” 2. Ð2 Ð1ĮXAMPLE 3 1 3 2 4 Given: Ð3 Prove: Ð4 Statements Reasons 1. Definition Angles.Ĩ Given: Ð2 Ð3 Prove: Ð1 Ð4 1. Vertical Angle Theorem Proof Prove: Ð2 Given: Ð1 and Ð2 are vertical angles. 1 3 4 2 NOTE: You cannot use the reason “Vertical Angle Theorem” or “Vertical Angles are Congruent” in this proof. Prove: Ð2 Given: Ð1 and Ð2 are vertical angles. Aside: Would the converse of this theorem work? If two angles are congruent, then the angles are vertical angles. Prove: Conclusion: The angles are congruent. Given: Hypothesis: Two angles are vertical angles. Ð3 and Ð4 are supplementary.ĥ Given: Prove: Vertical Angle Theorem: Vertical Angles are Congruent.Ĭonditional: If two angles are vertical angles, then the angles are congruent. Prove: Ð3 and Ð4 are supplementary 3 4 D E F Statements Reasons 1. Supplementary Angles add up to 180 m A+mLB180 Example: 110 xyr and L ryz are supplementary angles. Prove: Ð3 and Ð4 are supplementary 3ĮXAMPLE 2 Given: ÐDEF is a straight angle. A + B 180 degrees (supplementary angles) B + C 180 degrees (supplementary angles) (substitution) Using postulates and math properties, we construct a sequence of logical steps to prove a theorem. Definition of a right angle.Ĥ Given: ÐDEF is a straight angle.

(They are across from one another.)ģ EXAMPLE 1 Given: Ð1 and Ð2 are complementary
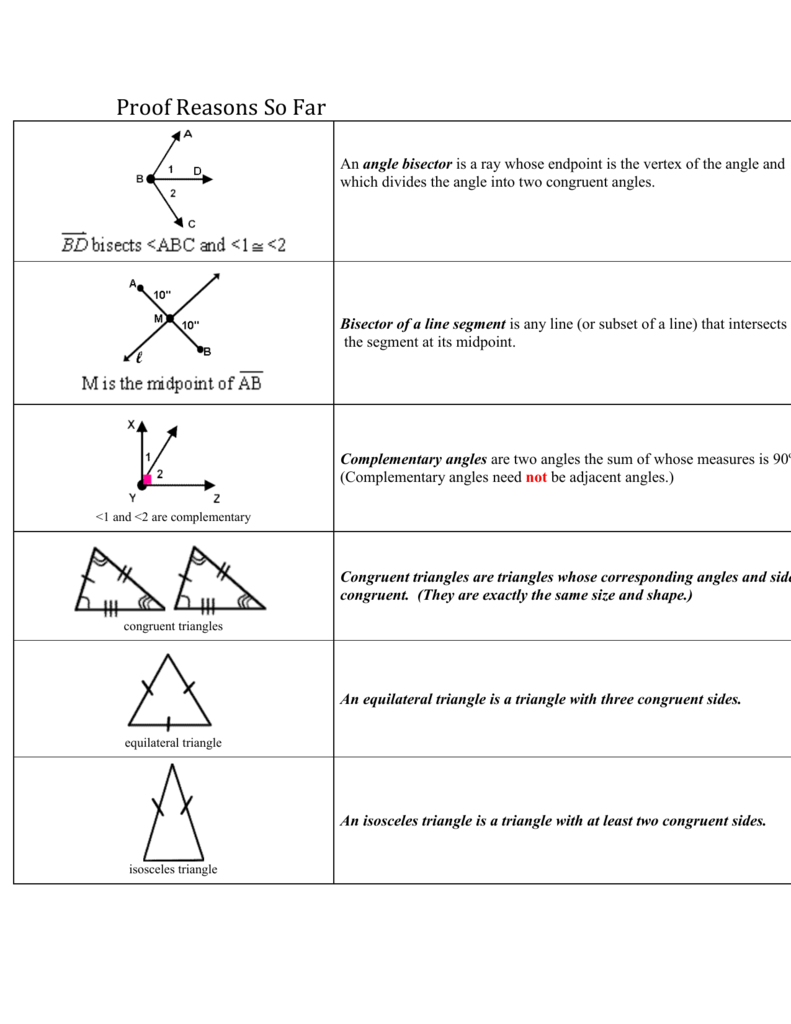
Vertical Angles: The two non-adjacent angles that are created by a pair of intersecting lines. Supplementary Angles: Two angles whose measures sum to 180. Complementary Angles: Two angles whose measures sum to 90. Straight Angle: An angle whose measure is 180. Right Angle: An angle whose measure is 90.


 0 kommentar(er)
0 kommentar(er)
